Deep learning 01--opencv, eigen and softmax regression, part 2--implementation details of softmax

    This post will record some implementation details of softmax regression, I will map the equation introduced by UFLDL(all of the images are come from here) and source codes on this post.

    First of all, to finish the classification tasks, we need a train function to train the data.

/**
 * @brief Train the input data by softmax algorithm
 * @param train Training data, input contains one\n
 *  training example per column
 * @param labels The label of each training example
 */
template<typename T>
void softmax<T>::train(const Eigen::Ref<const EigenMat> &train,
                       const std::vector<int> &labels)
{
    //#1 generate unique labels, because we need the
    //NumClass and generate the ground truth table
    auto const UniqueLabels = get_unique_labels(labels);
    auto const NumClass = UniqueLabels.size();
    
    //#2 initialize weight and gradient
    weight_ = EigenMat::Random(NumClass, train.rows());
    grad_ = EigenMat::Zero(NumClass, train.rows());

    //#3 initialize ground truth
    auto const TrainCols = static_cast<int>(train.cols());
    EigenMat const GroundTruth = get_ground_truth(NumClass, TrainCols,
                                                  UniqueLabels,
                                                  labels);

    //#4 create the random generator for mini-batch algorithm
    std::random_device rd;
    std::default_random_engine re(rd());
    int const Batch = (get_batch_size(TrainCols));
    int const RandomSize = TrainCols != Batch ?
                TrainCols - Batch - 1 : 0;
    std::uniform_int_distribution<int>
            uni_int(0, RandomSize);
    for(size_t i = 0; i != params_.max_iter_; ++i){
        auto const Cols = uni_int(re);
        auto const &TrainBlock =
                train.block(0, Cols, train.rows(), Batch);
        auto const &GTBlock =
                GroundTruth.block(0, Cols, NumClass, Batch);
        //#5 compute the cost of the cost function
        auto const Cost = compute_cost(TrainBlock, weight_, GTBlock);
        //#6 break the loop if meet the criteria
        if(std::abs(params_.cost_ - Cost) < params_.epsillon_ ||
                Cost < 0){
            break;
        }
        params_.cost_ = Cost;
        //#7 compute gradient
        compute_gradient(TrainBlock, GTBlock);
        //#8 update weight
        weight_.array() -= grad_.array() * params_.lrate_;
    }
}

    The most complicated part is #5 and #7, other part is trivial. To make #5 work, I need to finish the cost function(graph_00) and gradient descent(graph_01).

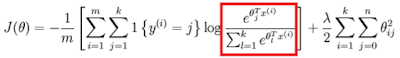graph_00

graph_01

    We can notice the hypothesis part(rounded by red suqare) may introduce very large value, this may cause the problem of overflow, to prevent this, we can do some preprocessing on it. The solution of UFLDL is subtract the largest large constant value from each of the terms before computing the exponential, this is trivial to be done in Eigen.

template<typename T>
void softmax<T>::compute_hypothesis(Eigen::Ref<const EigenMat> const &train,
                                    Eigen::Ref<const EigenMat> const &weight)
{    
    hypothesis_.noalias() = weight * train;
    max_exp_power_ = hypothesis_.colwise().maxCoeff();
    for(size_t i = 0; i != hypothesis_.cols(); ++i){
        hypothesis_.col(i).array() -= max_exp_power_(0, i);
    }

    hypothesis_ = hypothesis_.array().exp();
    weight_sum_ = hypothesis_.array().colwise().sum();
    for(size_t i = 0; i != hypothesis_.cols(); ++i){
        if(weight_sum_(0, i) != T(0)){
            hypothesis_.col(i) /= weight_sum_(0, i);
        }
    }
    //prevent feeding 0 to log function
    hypothesis_ = (hypothesis_.array() != 0 ).
            select(hypothesis_, T(0.1));
}

    After I have the hypothesis matrix, I can compute the cost and the gradient at ease.

template<typename T>
double softmax<T>::compute_cost(const Eigen::Ref<const EigenMat> &train,
                                const Eigen::Ref<const EigenMat> &weight,
                                const Eigen::Ref<const EigenMat> &ground_truth)
{    
    compute_hypothesis(train, weight);
    double const NSamples = static_cast<double>(train.cols());
    return  -1.0 * (hypothesis_.array().log() *
                    ground_truth.array()).sum() / NSamples +
            weight.array().pow(2.0).sum() * params_.lambda_ / 2.0;
}

template<typename T>
void softmax<T>::compute_gradient(Eigen::Ref<const EigenMat> const &train,
                                  Eigen::Ref<const EigenMat> const &weight,
                                  Eigen::Ref<const EigenMat> const &ground_truth)
{
    grad_.noalias() =
            (ground_truth.array() - hypothesis_.array())
            .matrix() * train.transpose();
    auto const NSamples = static_cast<double>(train.cols());
    grad_.array() = grad_.array() / -NSamples +
            params_.lambda_ * weight.array();
}

   The test results could see on this post.

Deep learning 00--opencv, eigen and softmax regression, part 1--use softmax to clasisify data

    Recently I am studying deep learning algorithms and try to implement some of them, there are many deep learning framework of c++ out there(ex : caffe), why do I try to build them by myself?the reasons push me to implement they are

1. This is a good way to study the algorithm
2. Not all of the deep learning library developed by c++ community are easy to build, more precisely, it is a pain to build them on some major platform(ex : windows), c and c++ community do not have a standard build system really is a big problem.

    The first algorithm I am trying to build is softmax regression based on the tutorial of UFLDL and softmax regression with opencv(I implement it with Eigen and opencv rather than matlab build in function).In this post I want to record how do I implement the softmax regression and show some results. I pick Eigen to help me implement the algorithms because it is

1. Portable and very easy to compile
2. Api are clean, easy to use and expressive
3. Performance is quite good
4. Well maintain, nice document 
5. Expression template rock 

    Softmax regression is a more general logistic regression, that is, logistic regression can classify two lables only, but sofmax regression can classify more than two labels. If this is the first time you try to implement an algorithm which involve a lot of matrix manipulation, you may overwhelm with the math equations, wondering how to write fast, clean vectorization codes. Following are some steps help me to develop the algorithms I want to share with you, take it as some reference materials but not golden rules.

1. Find a good matrix library, like Eigen or Armadillo
2. Study the algorithm carefully, make sure you understand every steps of it
3. Write down the matrix operations on a white paper, check the dimensions, the operations results of each step is reasonable or not, if you can not persuade yourself this result is meaningful, go back to step 2, do not bet on luck
4. Implement the algorithms
5. Run the gradient checking algorithms to check the result, if error, go back to step 2 or step 3
6.  Run on clean examples like MNIST, those examples already do preprocess for you
7. If the result are poor, try to tune the parameters or go back to step 2

    Ok, enough of talk, just show you some codes.

using namespace ocv::ml;

namespace{

using EMat = ocv::ml::softmax<>::EigenMat;

EMat read_data(std::string const &file)
{
    std::ifstream in(file);
    std::cout<<"read file\n";
    if(in.is_open()){
        std::cout<<"is open\n";
        EMat output(30, 284);
        for(size_t col = 0; col != output.cols(); ++col){
            for(size_t row = 0; row != output.rows(); ++row){
                in>>output(row, col);
            }
        }

        return output;
    }else{
        std::cout<<"cannot open file : "<<file<<"\n";
    }

    return softmax<>::EigenMat();
}

std::vector<int> read_label(std::string const &file)
{
    std::ifstream in(file);
    std::vector<double> output;
    //not the most efficient way, but easier to write
    std::copy(std::istream_iterator(in),
              std::istream_iterator(),
              std::back_inserter(output));

    return std::vector<int>(output.begin(),
                     output.end());
}

}

void softmax_test()
{
    ocv::ml::softmax<> sm;
    sm.train(read_data("softmax_train_data.txt"),
             read_label("softmax_train_label.txt"));
    auto const TestData =
            read_data("softmax_test_data.txt");
    auto const TestLabel =
            read_label("softmax_test_label.txt");
    double correct = 0;
    for(size_t i = 0; i != TestLabel.size(); ++i){
        auto const Result =
                sm.predict(TestData.block(0, i, TestData.rows(),
                                          1));
        if(Result == TestLabel[i]){
            ++correct;
        }        
    }

    std::cout<<"true positive pro : "<<
               (correct/TestLabel.size())<<"\n";
}

   This class use mini-batch to train the data, the results should within 89%~94%.The example use the ocv_libs of v1.1, the test data is located at here(I download from eric yuan).  The test example(softmax_test) is located at here(v1.0).

    Next post of deep learning will talk about the implementation details of this softmax class.